Matematik opg 1540 1543 1629 1635 1646

Indholdsfortegnelse

1 Opg 1540
2 Opg 1543
3 Opg 1629
4 Opg 1635
- 4.1 Alternativ beregning
5 Opg 1646

Opg 1540

Find tallet k, så vektorene b og c er lige lange.

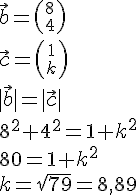
$LaTex: \vec{b} = {8\choose 4}\\ \vec{c} = {1\choose k}\\ |\vec{b}| = |\vec{c}| \\ 8^2+4^2=1+k^2 \\ 80 = 1 + k^2 \\ k = \sqrt{79} = 8,89$

Opg 1543

Find tallet k, så vektorene b bliver dobbelt så lang som vektoren c.

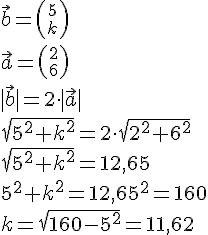
$LaTex: \vec{b} = {5\choose k}\\ \vec{a} = {2\choose 6}\\ |\vec{b}| = 2\cdot|\vec{a}| \\ \sqrt{5^2+k^2}=2 \cdot \sqrt{2^2+6^2} \\ \sqrt{5^2+k^2}=12,65 \\ 5^2+k^2=12,65^2 = 160 \\ k = \sqrt{160-5^2} = 11,62$

Opg 1629

En femkant ligger udspændt mellem punkterne A,B,C,D og E. Vi skal bestemme vinklen til D og vinklen mellem diagonalerne AC og BE.

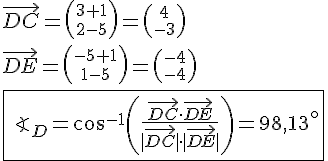
$LaTex: \vec{DC} = {3+1 \choose 2-5} = {4 \choose -3}\\ \vec{DE} = {-5+1 \choose 1-5} = {-4 \choose -4}\\ \fbox{\angle_{D}=\cos^{-1}\left(\frac{\vec{DC}\cdot\vec{DE}}{|\vec{DC}|\cdot |\vec{DE}|}\right) = 98,13^{\circ}}\\$

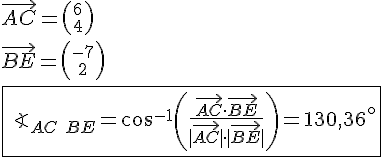
$LaTex: \vec{AC} = {6 \choose 4}\\ \vec{BE} = {-7 \choose 2}\\ \fbox{\angle_{AC\ BE}=\cos^{-1}\left(\frac{\vec{AC}\cdot\vec{BE}}{|\vec{AC}|\cdot |\vec{BE}|}\right) = 130,36^{\circ}}\\$

Opg 1635

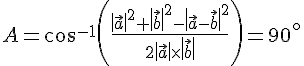
$LaTex: A = \cos ^{ - 1} \left( {\frac{{\left| \vec{ a } \right|^2 + \left| \vec{ b } \right|^2 - \left| \vec{ a } - \vec{ b } \right|^2 }}{{2\left| \vec{ a } \right| \times \left| \vec{ b } \right|}}} \right)= 90^\circ$

Alternativ beregning

Først skal vi finde krydsproduktet:

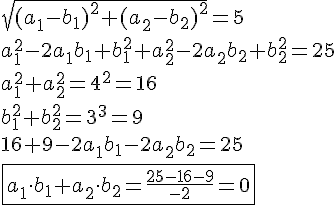
$LaTex: \sqrt{(a_1-b_1)^2+(a_2-b_2)^2} = 5\\ a_1^2-2a_1b_1+b_1^2+a_2^2-2a_2b_2+b_2^2 = 25\\ a_1^2+a_2^2 = 4^2 = 16\\ b_1^2+b_2^2 = 3^3 = 9\\ 16+9-2a_1b_1-2a_2b_2 = 25\\ \fbox{a_1\cdot b_1+a_2\cdot b_2 = \frac{25-16-9}{-2} = 0}$